Manage your design uncertainties better bu leveraging CAE early in design process
Static Analysis
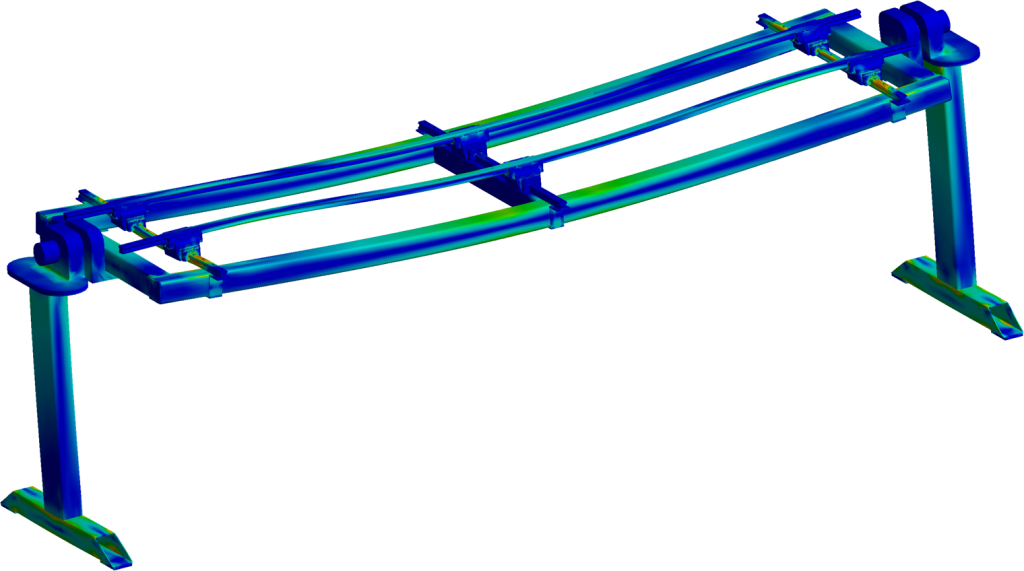
Static structural analysis is the most widely used FE methodology to understand the deformation, stress and strain of an assembly or a component under investigation, for a range of loads which ensures structural integrity of the system.
Static structural FE analysis is the most effective structural study with the least consumption of man-machine hours in comparison with other type of analysis. And it produces much more detailed understanding of structural behavior than experimental investigation which is quick and less expensive to investigate.


Model Analysis
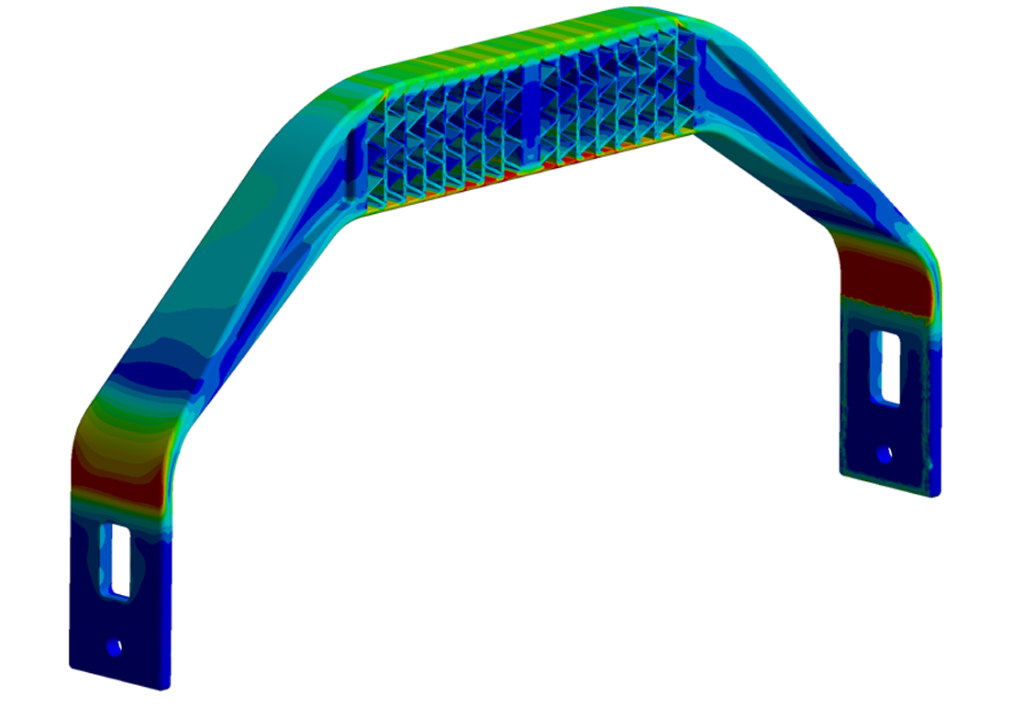
Modal Analysis simulates deformation of a structural assembly or a component when excited by external vibrational loads. It is used to determine the structure’s dynamic characteristics like natural resonant frequencies, damping factors and the associated pattern of structural deformation called mode shapes.
We also provide a three dimensional graphic representation of different mode shapes which identifies the locations of soft spots on the structure. Identifying such locations can provide engineers or designers to place additional equipment for stability and minimising structural failure due to resonance.
To help understand the output of Modal analysis,
- We create animated outputs in .gif or .mp4 format of different model shapes
- The Modal mass participation factor
- Pin-pointing the sweet spots in the system or the structural assembly, helping to show the results clearly

Harmonic Analysis
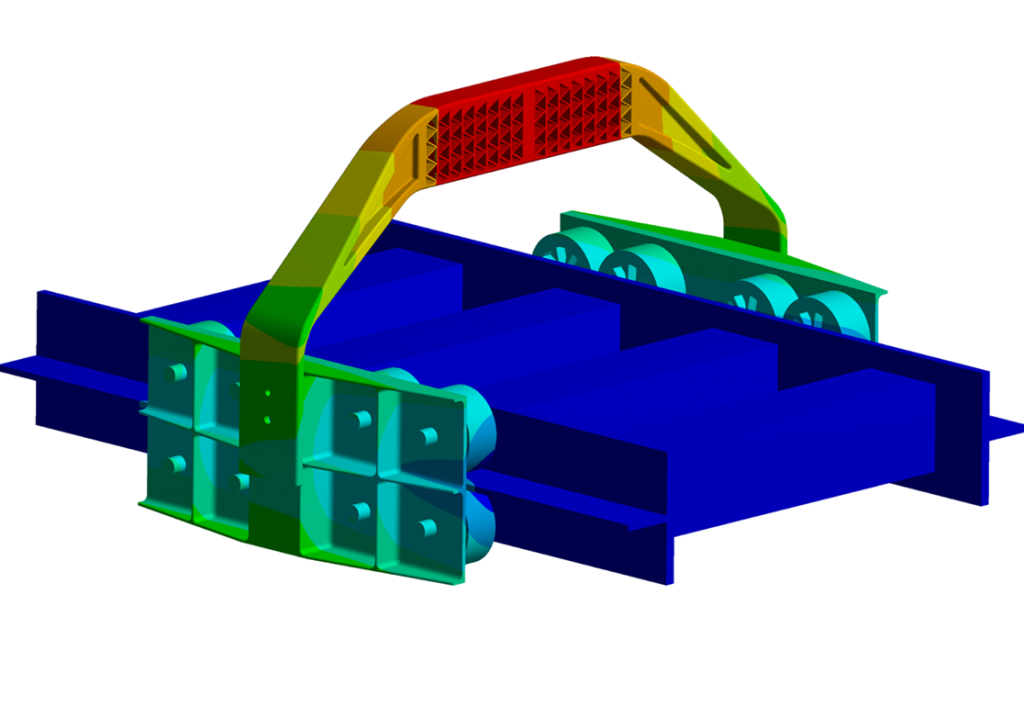
In a structural assembly, any load which is cyclical in nature produces a sustained cyclical harmonic response. Harmonic FE Analysis study helps them to determine the steady-state response of the structural system where the loads vary sinusoidally with time.
Harmonic or Frequency response analysis subjects the model under investigation to constant vibrational load frequency. It uses results from Modal analysis and the corresponding natural frequencies to determine the response of the model for a specific frequency range.
This analysis technique enables you to investigate whether the structural assembly will withstand –
- The probability of resonance due to induced vibration
- Fatigue life of the component or assembly
- And other effects of Harmonic loads such as Principal stresses and deformations

Random Vibration Analysis
Random Vibrational Analysis or Power Spectral Density (PSD) subjects the model under investigation to random vibrational loads. Unlike Harmonic vibrational loads these loads are non-periodic and contains multitude of frequencies. An example would be the response of an ECU mounted in a truck, subjected to the vibration from engines, road roughness, acoustic pressure etc.
The input load for the analysis are always non-deterministic, i.e. the time history of each load is unique every time and hence can only be in multitude of frequencies.
The output for the analysis such as deformation, stresses are always statistical in nature.

Seismic Analysis
Seismic analysis or Random Spectrum analysis (RSA) is similar to PSD, but its input is defined rather than random. RSA is often used to evaluate the structure’s response to sudden jolt or a shock or maximum response based upon the input response spectrum.
Through RSA, structure’s inelastic behavior and failure pattern in severe seismic events can be determined


Thermal Analysis
A good understanding of thermal distribution and loads is often required to understand the system working under elevated temperature which can lead to unexpected high thermal stresses and strains which may lead to failure.
Thermal analysis is often performed using CFD and FEA. CFD is preferred to understand the boundary conditions due to flow of fluid and FEA is performed to evaluate the thermal stresses and strain in the system under steady-state or Transient conditions.
Steady and Transient FEA thermal study can be used to determine the thermal distribution in an object where the loads can either dependent or independent with time. Heat transfer study through the object can also always occur through conduction, convection and radiation.
Through thermal analysis we can provide bulk of information on –
- Thermal distributions on the object of study
- Thermal induced stress and stress concentrated regions
- Thermal induced deformation
- Heat flux paths for solids and insulations

Non-Linear Analysis
Majority of FEA study assume material non-linearity where the ratio of stress to strain is always assumed to be constant. However, when the stress levels in the component exceeds the material yield point, the stress-strain relation will no longer linear, the material moves into plastic region and therefore Non-Linear FEA study is required to simulate the stress and deformation of the component accurately.
Geometric Non-linearity
Non-linear analysis becomes necessary when stiffness of the part changes. As a rule of thumb non-linear analysis is considered when the deformations are larger than 1/20th of the largest dimension of the assembly. If the stiffness changes due to shape change then the behavior is called geometric non-linearity.
Material Non-linearity
If the stiffness changes due to material properties or if the strains are very high as in case of rubbers and elastomers or if the loads are very high to cause permanent deformation in the components as in case of plastics, then a non-linear material model is to be used.
Contact Non-linearity
In FE analysis, a contact between two components are defined as Linear and Non-linear contacts. Linear contact is widely used where the definition of contacts between two adjacent components has no relative motion. Whereas on the other hand, Non-linear contact analysis allows separation of contacts, an iterative process is involved in calculating non-linear contacts and hence demands high computational efforts.

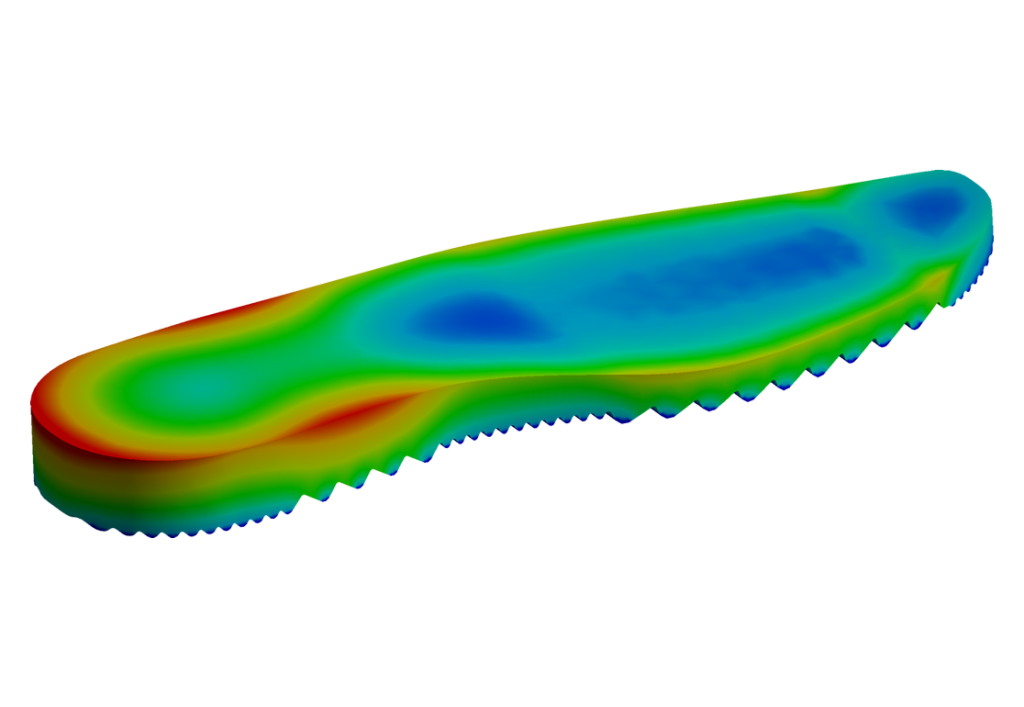
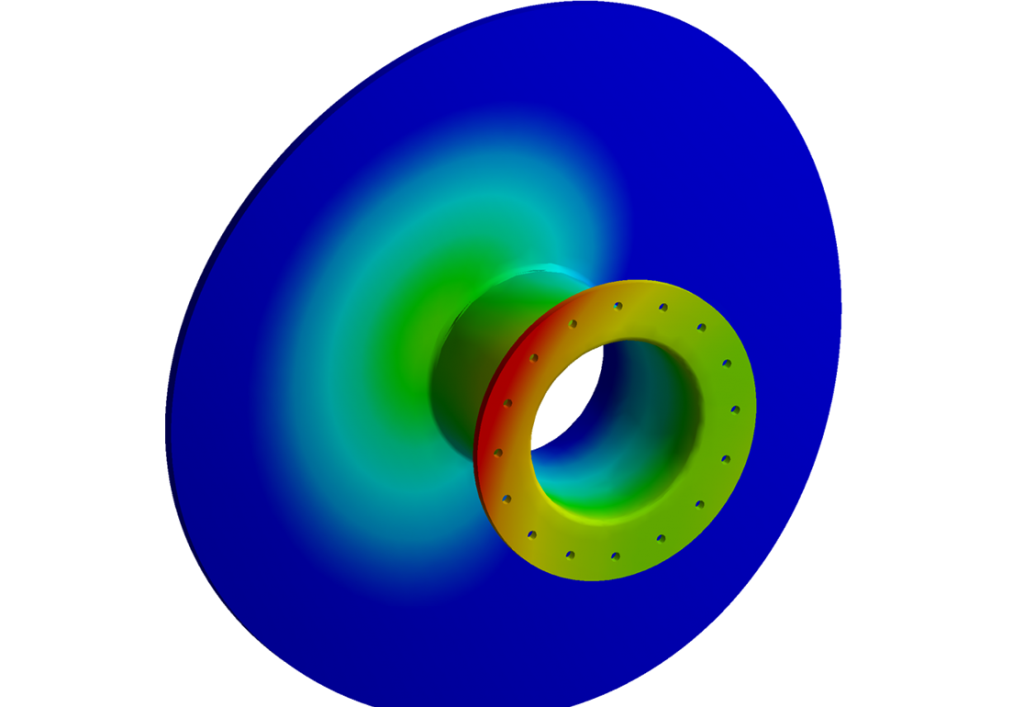
Stress linearization
General primary membrane Equivalent Stress (Pm)
Average primary stress across solid section. Excludes dis-continuities and concentrations. Produced only by mechanical loads.
Local Primary Membrane Equivalent Stress (PL)
Average stress across any solid section. Considers dis-continuities not concentrations. Produced only by mechanical loads.
Primary Bending Equivalent Stress (Pb)
Component of primary stress proportional to distance from the centroid of solid section. Excludes dis-continuities and concentrations. Produced only by mechanical loads.
Secondary Membrane plus bending intensity (Q)
Self-equilibrating stress necessary to satisfy continuity of structure. Occurs at structural discontinuities. Can be caused by mechanical load or by differential thermal expansion. Excludes local stress concentrations.


